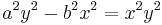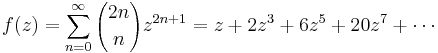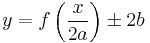Bullet-nose curve

In mathematics, a bullet-nose curve is a unicursal quartic curve with three inflection points, given by the equation

$a^2y^2-b^2x^2=x^2y^2 \,$

The bullet curve has three double points in the real projective plane, at x=0 and y=0, x=0 and z=0, and y=0 and z=0, and is therefore a unicursal (rational) curve of genus zero.

$f(z) = \sum_{n=0}^{\infty} {2n \choose n} z^{2n%2B1} = z%2B2z^3%2B6z^5%2B20z^7%2B\cdots$

then

$y = f\left(\frac{x}{2a}\right)\pm 2b\$

are the two branches of the bullet curve at the origin.

References

J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. pp. 128–130. ISBN 0-486-60288-5.